Summer is the golden time to prepare for the American Math Competitions!
The period of time between 4th-8th grade is most critical to the development of students’ mathematical fascinations, interests, and skills!
- 2024 AMC 8: 10 perfect scorers. 54 students got the DHR. 29 students got the HR.
- 2023 AMC/AIME: 99 AIME qualifiers. 1 AMC 10 perfect scorer. 1 AMC 12 perfect scorer.
- 2023 JMO/AMO: 8 USAMO Awardees and 7 USAJMO Awardees
- 1 USAMO Gold Award, 1 USAMO Silver Award, 4 USAMO Bronze Awards, and 2 USAMO Honorable Mention Awards.
- 1 USAJMO Top Winner, 1 USAJMO Winner, and 5 USAJMO Honorable Mention Awards.
- 2023 MOP: 4 MOP winners.
- How to Prepare for the AMC 8
Summer Session I (Counting and Probability)
8 Classes (Eastern Time: 1:00 – 4:00 pm), Total: 24 Hours
6/8, 6/9, 6/15, 6/16, 6/22, 6/23, 6/29, 6/30 (Mock Exam/Review)
Summer Session II (Number Theory)
8 Classes (Eastern Time: 1:00 – 4:00 pm), Total: 24 Hours
7/6, 7/7, 7/13, 7/14, 7/20, 7/21, 7/27, 7/28 (Mock Exam/Review)
Online Registration is now open! Click HERE to register and pay.
| Tuition (including all materials) | |
| Session I (24 Hours) | |
| New Student: | Via Zelle: $840 (Phone: 240-406-3402) Please include your child’s name and “AMC 8 Summer I” in the “Memo” box. |
| Via PayPal: $870 |
|
| Returning Student: | Via Zelle: $825 (Phone: 240-406-3402) Please include your child’s name “AMC 8 Summer I” in the “Memo” box. |
| Via PayPal: $855 |
|
| Session II (24 Hours) | |
| New Student: | Via Zelle: $840 (Phone: 240-406-3402) Please include your child’s name “AMC 8 Summer II” in the “Memo” box. |
| Via PayPal: $870 |
|
| Returning Student: | Via Zelle: $825 (Phone: 240-406-3402) Please include your child’s name “AMC 8 Summer II” in the “Memo” box. |
| Via PayPal: $855 |
|
| Sessions I & II (48 Hours) | |
| New Student: | Via Zelle: $1,655 (Phone: 240-406-3402) Please include your child’s name and “AMC 8 Summer I and II” in the “Memo” box. |
| Via PayPal: $1,715 |
|
| Returning Student: | Via Zelle: $1,635 (Phone: 240-406-3402) Please include your child’s name and “AMC 8 Summer I and II” in the “Memo” box. |
| Via PayPal: $1,695 |
|
| Click HERE to see payment and refund policy. | |
- This is a live class, not a pre-recorded one. Instructors will ask students questions, and students can also ask questions during the class or email their questions to instructors after class.
- We record all of our lessons as a big bonus so that our students can watch class videos after class for review and self-study.
This year’s AMC 8 contest contains 5 number theory problems and 6 counting & probability problems. In last year’s AMC 8/MathCounts Prep Summer Weekend Course about Discrete Math (Number Theory, Counting, and Probability), we extensively discussed typical examples that are the same as or very similar to all these problems so that our students can become very familiar with them and fully master those powerful methods to solve them. This is how our course can greatly help our students to get a high score on the AMC 8 test!
You are very welcome to sign up for our online course which offers a quick, efficient way for students to interact with teachers over long distance. We use the Google Meet to video chat and easily connect with students to teach them our tricks and shortcuts to getting an amazing score on their contests, as well as offer them our guidance and support. Students can ask questions face-to-face via Google meet, and can complete problems with the supervision of our teachers/coaches. Click HERE to see detailed instruction.
A commitment to the whole course can maximize the benefit of learning all the math ideas, methods, strategies, tactics, skills, and techniques. Click HERE to see attendance/absence/aancellation/makeup lesson policy
- We will help students gain a deeper understanding of the fundamental math concepts, build a solid foundation in math, and develop the critical thinking and problem-solving skills different from those in the school classes, motivation, and perseverance for reaching their full potential.
- We will focus on efficient tricks, shortcuts, and strategies to solve competitive math problems as well as test-taking tactics.
- The emphasis of this class will be on comprehensive problem-solving in discrete math (number theory, counting, and probability), which is very common in competitive math, but is not included in school curriculum. See more at: Why Discrete Math is very Important
- We will utilize a highly effective teaching model as described in the article: Small-sized Class Instruction-focused Model.
Instructor: Dr. Henry Wan

Purpose: To prepare for math competitions, such as
- AMC 8 — Thursday, January 16, 2025.
- MATHCOUNTS
- Math Kangaroo Contest
- Math Olympiads for Elementary and Middle Schools (MOEMS)
Contact Information:
Ivy League Education Center
Tel: 240-300-4380
Email: chiefmathtutor@gmail.com

Specific Goal of the 2025 AMC 8:
To become part of the top 5% of scorers on the AMC 8, and then receive National Honor Roll Certificates.
Specific Goal of the 2024 AMC 10:
To earn a score of 90 or more out of 150 on the AMC 10, and then receive National Achievement Honor Roll Certificates.
Specific Goal of the MathCounts:
To become one of the top winners in the individual competition at the chapter level and then advance to the state competition.

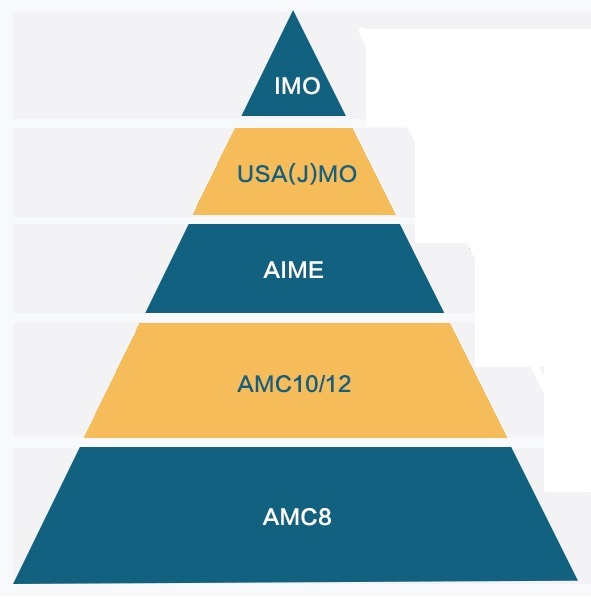
There are many math competitions in the United States. Of those, only
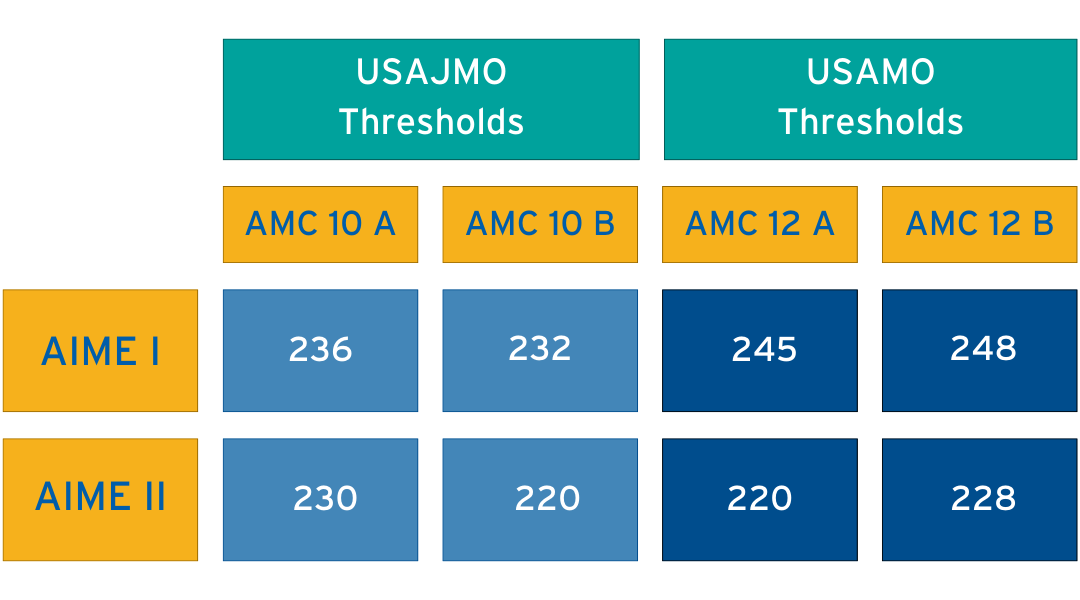
AMC → AIME → USAMO sequence
would take you to the IMO (International Math Olympiad), the highest level math competition for high school students in the world!

Description:
Our curriculum focuses on advancing the mathematical skills of 5th-8th graders to prepare them for math competitions, such as AMC 8, AMC 10, Mathcounts, Math Olympiads for Elementary and Middle Schools (MOEMS), Math Kangaroo, and Math League. A variety of contest questions, including all past official AMC 8 problems, the first 15 problems on each old AMC 10 tests, and MathCounts Competition problems at the school, chapter, state, and national level, are used to teach students strategies to solve problems and help students prepare for the competitions. These problems stimulate their interest and enthusiasm for critical thinking and problem solving, broaden their mathematical intuition, and develop their brainpower. The topics taught in this class are not covered in regular school math classes, allowing our students to stay one step ahead.

Benefits:
- 16 tutorial handouts (640 pages) developed by Dr. Henry Wan and 500 new problems similar to AMC 8 level from the licensed AMC Database. Click HERE to see a typical class handout sample we developed.
- 4 FREE mock tests, each of which has 25 questions taken from the licensed AMC Database. Mock tests are calibrated to be at the same difficulty level as the real AMC 8. Surprisingly, some problems in our previous mock tests appeared in the recent official AMC 8 tests, as shown at:
- FREE registration for the AMC 8 Contest on January 16, 2025. Please see: The Online AMC 8 Contest at the Ivy League Center on January 16, 2025
- FREE registration for the AMC 10A — November 10, 2024 and AMC 10B — November 16, 2024. Please see: The AMC 10/12 Contests on November 10, 2024, and November 16, 2024
Grade Levels: Rising Grades 4-8

This class focuses on efficient tricks, shortcuts, and strategies to solve competitive math problems as well as test-taking tactics. The emphasis of this class will be on comprehensively problem-solving in discrete math (number theory, counting, and probability), which is the most important to competitive math. We reserve the right to adjust the teaching content and pace according to the actual performance of students .
Session I (Counting and Probability)
| Class | Date | Topic |
| 1 | 6/8, Sat | Counting with Sets and Venn Diagrams |
| 2 | 6/9, Sun | Counting with Factorials, Permutations, and Combinations |
| 3 | 6/15, Sat | Counting with Pascal’s Triangle, Pascal Patterns, and Hockey Sticks |
| 4 | 6/16, Sun | Counting Paths on a Graph |
| 5 | 6/22, Sat | Casework Counting |
| 6 | 6/23, Sun | Stars and Bars Method, and Integer Equations |
| 7 | 6/29, Sat | Counting Techniques in Probability |
| 8 | 6/30, Sun | Counting with Patterns |
Session II (Number Theory)
| Class | Date | Topic |
| 1 | 7/6, Sat | Divisibility Rules |
| 2 | 7/7, Sun | Factor Trees and Prime Factorization |
| 3 | 7/13, Sat | Counting Divisors |
| 4 | 7/14, Sun | Greatest Common Divisors, and Least Common Multiples |
| 5 | 7/20, Sat | Units Digits in Arithmetic |
| 6 | 7/21, Sun | Patterns in the Last Two Digits of a Power |
| 7 | 7/27, Sat | Base Numbers, Base Number Digits, and Converting Integers Between Bases |
| 8 | 7/28, Sun | Modular Arithmetic and Linear Congruences |
Homework:
The focus will be on the final 15 problems on the AMC 8, and the first 10 problems on the AMC 10, as well as those Those medium and hard-level difficulty questions on the MathCounts. We will provide students with 500 brand new problems, extracted from the licensed AMC Database, having similar difficulty and style as the hard real AMC 8 problems.
Read more at:
- Problem 23 on the 2023 AMC 8 is Exactly the Same as a Problem on Our 2022 AMC 8 Mock Test
- Some Hard Problems on the 2023 AMC 8 are Exactly the Same as Those in Other Previous Competitions
- Two Problems on the 2020 AMC 8 are Exactly the Same as Two Problems on Our Sample 2017 AMC 8 Mock Test
- Some Hard Problems on the 2016 AMC 8 are Exactly the Same as Previous Problems on the AMC 10/12 and the Other Competitions
- The Hardest Problems on the 2017 AMC 8 are Extremely Similar to Previous Problems on the AMC 8, 10, 12, Kangaroo, and MathCounts
- The Hardest Problems on the 2018 AMC 8 are Nearly Identical to Former Problems on the AMC 8, 10, 12, and MathCounts
On average, at least 6 hours per week, as described in the article: Homework assignments are a fundamental part of our courses. Click HERE to see a typical homework sample we developed. Each week, we will carefully review and check 3 students’ homework, and correct any mistakes. The next week, we will check another 3 students’ homework, and this will continue on a rotational basis until all students have had their homework checked at least once and the cycle will start again. Based on the work of the 3 students that week, we will provide the those 3 students with individualized proposal and support. More details can be found in the article: Homework Correction is very Important — We Give an Extensive Correction of the Incorrect Answers of All Homework.

We have to face the simple truth that to do well on these grueling contests, we will need to practice. Just like it is for sports and music, the key to success is repetition and practice. We strongly believe in effort and the malleability of intelligence. Intelligence can be enhanced through effort. People can develop impressive levels of expertise through hard work and practice. Effort and persistence are the keys to success. Hard work always pays off: practice makes perfect!
All problems from past AMC 8 exams (1985-2024), AMC 10 exams (2000-2023), and MathCounts (1990–2024) form our “big data” system. Based on artificial intelligence (AI), machine learning, and deep learning, we devised a data mining and predictive analytics tool for math problem similarity searching. Using this powerful tool, we examined the types, styles, frequencies, characteristics, and traits of questions in all these materials, and then completely “decoded” the AMC, and MathCounts. We always completely show all the “secret code” cracked from the above big data to our students, and teach them to totally grasp and “control” the AMC and MathCounts. For all questions on the recent AMC/MathCounts contests, we can find their “ancestors” and “roots” from the old AMC/MathCounts problems. Therefore, the best way to prepare for the contest is to practice by solving old AMC/MathCounts problems.

Main Purpose:
Our main purpose is to help our students gain deeper understanding of the fundamental math concepts, build a solid foundation in math, and develop the critical thinking and problem-solving skills that are so valuable to success in any career. We are big believers in the FUNDAMENTALS! Our students will receive the LIFELONG BENEFITS from learning math.
Regardless of his/her math level, each student will have the opportunity to learn math in a fun, friendly, cooperative, supportive learning environment. The most important thing is to have fun, playful, and enjoyable!

Our Students
In 2024, we had 90 students who obtained top scores on the AMC 8 contest!
- 10 of our students were among the top 116 worldwide winners (Perfect Scorers).
- 54 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers. They were among the 697 worldwide winners.
- 29 students received National Honor Roll Certificates awarded to top 5% test takers. They were among the 2,683 worldwide winners.
- 93 out of our 96 students (96.9%) received National Awards for the AMC 8 from the Mathematical Association of America
Read more at: 2024 AMC 8 Results Just Announced — Ten Students Received Perfect Scores
In 2023, we had 99 students who qualified for the AIME either through the AMC 10A/12A or the AMC 10B/12B. One of our students was among the 11 Perfect Scorers worldwide on the AMC 10B: Ali R. and one of our students was among the 13 Perfect Scorers worldwide on the AMC 12B: Yaoyun X. Read more at: 99 Students Qualified for the 2024 AIME and 2 Students Received Perfect Scores on the 2023 AMC 10/12
In 2023, we had 8 students who won USAMO awards and 7 students who won USAJMO awards.
- 1 USAMO Gold Award, 1 USAMO Silver Award, 4 USAMO Bronze Awards, and 2 USAMO Honorable Mention Awards.
- 1 USAJMO Top Winner, 1 USAJMO Winner, and 5 USAJMO Honorable Mention Awards.
Read more at: 2023 USAMO and USAJMO Awardees Announced — Congratulations to Eight USAMO Awardees and Seven USAJMO Awardees
In 2023, we had 90 students who obtained top scores on the AMC 8 contest!
- 8 of our students were among the top 81 worldwide winners (Perfect Scorers).
- 51 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers. They were among the 697 worldwide winners.
- 31 students received National Honor Roll Certificates awarded to top 5% test takers. They were among the 2,571 worldwide winners.
- 90 out of our 93 students (96.8%) received National Awards for the AMC 8 from the Mathematical Association of America.
Read more at: 2023 AMC 8 Results Just Announced — Eight Students Received Perfect Scores
In 2022, we had 96 students who qualified for the AIME either through the AMC 10A/12A or the AMC 10B/12B. One of our students was among the 6 Perfect Scorers worldwide on the AMC 10A: Justin W. and one of our students was among the 3 Perfect Scorers worldwide on the AMC 12B: Ming Y. Read more at: 96 Students Qualified for the 2023 AIME and 2 Students Received Perfect Scores on the 2023 Fall AMC 10/12
In 2022, we had 3 students qualified for the Math Olympiad Summer Program. Read more at: Brendon J., Kyle S., and Isabella Z. Qualified for the 2022 Math Olympiad Summer Program
In 2022, we had 1 student Competes in International Girls’ Math Olympiad. Read more at: sabella Z. Competes in International Girls’ Math Olympiad
In 2022, we had 7 students qualified for the USAMO and 7 students for the USAJMO. Read more at: 2022 USAMO and USAJMO Qualifiers Announced — Seven Students Qualified for the USAMO and Seven Students for the USAJMO.
In 2022, we had 88 students who obtained top scores on the AMC 8 contest!
- 10 of our students were among the top 131 worldwide winners (Perfect Scorers), as shown in Table 1. Click Here see a full list of the 131 worldwide winners.
- 52 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers. They were among the 1,010 worldwide winners. Click HERE see a full list.
- 26 students received National Honor Roll Certificates awarded to top 5% test takers. They were among the 2,449 worldwide winners. Click HERE see a full list.
- 88 out of our 91 students (96.7%)received National Awards for the AMC 8 from the Mathematical Association of America
Read more at: 2022 AMC 8 Results Just Announced — Ten Students Received Perfect Scores
In Fall 2021, we had 93 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. One of our students was among the 5 Perfect Scorers worldwide on the AMC 10A: Nina L. and one of our students was among the 2 Perfect Scorers worldwide on the AMC 10B: Ming Y. Read more at: 93 Students Qualified for the 2021 Fall AIME and 2 Students Received Perfect Scores on the 2021 Fall AMC 10/12
In 2021, we had 6 students qualified for the USAMO and 6 students for the USAJMO. Read more at: 2021 USAMO and USAJMO Qualifiers Announced — Six Students Qualified for the USAMO and Six Students for the USAJMO
In Spring 2021, we had 91 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. Two of our students was among the 17 Perfect Scorers worldwide on the AMC 12A: Evan L. and Suraj O. and one of our students was among the 27 Perfect Scorers worldwide on the AMC 10A: Xinchen L. Read more at: 91 Students Qualified for the 2021 AIME and 3 Students Received Perfect Scores on the 2021 AMC 10/12
In 2021, we had 8 students who got into the MathCounts state-level top 10. Yunyi L. won 9th Place in the 2021 MathCounts National Competition!
In 2020, we had 79 students who obtained top scores on the AMC 8 contest!
- 5 of our students were among the top 57 worldwide winners (Perfect Scorers).
- 49 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers.
- 25 students received National Honor Roll Certificates awarded to top 5% test takers.
- 79 out of our 81 students (97.5%) received National Awards for the AMC 8 from the Mathematical Association of America.
Read more at: 2020 AMC 8 Results Just Announced — Five Students Received Perfect Scores
In 2020, we had 82 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. One of our students was among the 11 Perfect Scorers worldwide on the AMC 12A: Yiyang X, and one of our students was among the 13 Perfect Scorers worldwide on the AMC 10A: Jason W.. 43 middle schoolers and 9 elementary schoolers qualified for the AIME!
In 2019, we had 71 students who obtained top scores on the AMC 8 contest!
- 8 of our students were among the top 151 National Winners (Perfect Scorers), including 2 sixth graders.
- 36 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers, as shown in Table 2.
- 27 students received National Honor Roll Certificates awarded to top 5% test takers, as shown in Table 3.
- 71 out of our 73 students (97.3%) received National Awards for the AMC 8 from the Mathematical Association of America
Read more at: 2019 AMC 8 Results Just Announced — Eight Students Received Perfect Scores
In 2019, we had 4 Students Qualified for the USAMO and 4 Students for the USJMO.
- Of the 280 USA Math Olympiad national qualifiers, 4 are our students: Luke C., Zipeng L., Sameer P., and Peter P.
- Of the 235 USA Junior Math Olympiad national qualifiers, 4 are our students: Michael H., Noah W., Holden W., and Isabella Z.
Read more at: 2019 USAMO and USAJMO Qualifiers Announced — Four Students Qualified for the USAMO and Four Students for the USAJMO
In 2019, we had 76 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. One of our students was among the 22 Perfect Scorers worldwide on the AMC 10A: Noah W. and one of our students were among the 10 Perfect Scorers worldwide on the AMC 12B: Kenneth W. Very impressively, 32 middle schoolers and 7 elementary schoolers qualified for the AIME!
In 2018, we had 64 students who obtained top scores on the AMC 8 contest!
- 3 of our students were among the top 44 National Winners (Perfect Scorers): Eric B., Kevin Y., and Isabella Z.
- 40 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers.
- 21 students received National Honor Roll Certificates awarded to top 5% test takers.
- 64 out of our 66 students (96.5%) received National Awards for the AMC 8 from the Mathematical Association of America
Read more at: 2018 AMC 8 Results Just Announced — Three Students Received Perfect Scores
In 2018, we had 73 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. Two of our students were among the 35 Perfect Scorers worldwide on the AMC 10A: Austen M. and Jason W. and two of our students were among the 21 Perfect Scorers worldwide on the AMC 12B: Kaan D. and Edward W. Remarkably, 11 middle schoolers and 2 elementary schoolers qualified for the AIME!
In 2017, we had 63 students who earned top scores on the AMC 8 contest!
- 7 of our students were among the top 75 National Winners (Perfect Scorers).
- 34 students received National Distinguished Honor Roll Certificates awarded to top 1% test takers.
- 22 students received National Honor Roll Certificates awarded to top 5% test takers.
- 63 out of our 65 students (97%) received National Awards for the AMC 8 from the Mathematical Association of America
Read more at: 2017 AMC 8 Results Just Announced — Seven Students Received Perfect Scores
In 2017, we had 61 students who are qualified to take the AIME either through the AMC 10A/12A or AMC 10B/12B. One of our students was among the 28 Perfect Scorers worldwide on the AMC 10A: Austen M., and two of our students were among the 65 Perfect Scorers worldwide on the AMC 10B: Ashwin A. and Brad Z. Remarkably, eight middle schoolers and one elementary schooler qualified for the AIME, which is geared toward high school students. Very impressively, Bryan Z., a 6th grader, gained a score of 132 out of 150 on the AMC 10B.Read more at: 2017 AIME Qualifiers Announced — 61 Students Qualified for the AIME
In 2016, we had 36 students who are qualified to take AIME either through AMC 10A/12A or AMC 10B/12B. One of our students was among the 23 Perfect Scorers worldwide on the AMC 10A: Joel (Junyao) T. Particularly, seven middle schoolers and one elementary schooler qualified for the AIME, which is geared toward high school students. Pravalika P., a 6th grader, got a 115.5 out of 150 on the AMC10B, which is very impressive. Read more at: 2016 AIME Qualifiers Announced — 36 Students Qualified for AIME
2011 – 2015: In total, 37 students scored above 120 on the American Mathematics Contest 10 (AMC 10) and qualified for the American Invitational Mathematics Examination (AIME); 26 students scored above 100 on the American Mathematics Contest 12 (AMC 12) and qualified for the American Invitational Mathematics Examination (AIME); 3 students qualified for the USA Mathematical Olympiad (USAMO), the highest level of math competition for high school students in the USA
2011 – 2015: In total, 23 students achieved perfect scores of 28 on the AMC 8
Read more at: Notable Achievements of Our Students

Our Uniqueness
We have a long history of close collaboration with the MAA’s American Mathematics Competitions (AMC), which are dedicated to strengthening the mathematical capabilities of our nation’s youth, and are the first of a series of competitions in high school mathematics that determine the United States team for the International Mathematical Olympiad (IMO).
We are only one in the Washington DC metropolitan area to offer elementary, middle, and high-school level competition math courses. Our students have received top scores and awards at prestigious national and math competitions.
Great Benefits of Math Competitions
In an increasingly competitive college application pool, the process of mastering math skills through our courses and participating in the American Math Competitions will help students strengthen and diversify their extracurricular activities. These contests can motivate students’ interest and passion in math, and they can discover their talent through solving challenging problems different from those in the school classes. Many top colleges also request AMC scores as part of the college application process. Both MIT and Caltech have entry blanks on their official admission application forms for the applicant to enter their best AMC and AIME scores. Ivy League Colleges and Stanford ask for to the AMC and AIME scores in their Supplement to the Common Application Forms. Your children deserve the chance to list these scores on their applications! Good AMC scores will greatly enhance admission opportunities for students to elite colleges.
- 2020 AMC 8 Results Just Announced — Five Students Received Perfect Scores
- Yunyi L. Won the 9th Place in the 2021 Mathcounts National Competition!
- 2020 AMC 8 Honor Roll and Honor Roll of Distinction Cut-off Scores
- 2020 AMC 8 Problem Topics
- Two Problems on the 2020 AMC 8 are Exactly the Same as Two Problems on Our Sample 2017 AMC 8 Mock Test
- 2020 AMC 8 Honor Roll and Distinguished Honor Roll Predicted Cut-off Scores
- 2020 AMC 8 Problems and Answers
- 2019 AMC 8 Results Just Announced — Eight Students Received Perfect Scores
- 2019 AMC 8 Problems and Answers
- The Hardest Problems on the 2018 AMC 8 are Nearly Identical to Former Problems on the AMC 8, 10, 12, and MathCounts
- 20 Sets of AMC 8 Mock Test with Detailed Solutions
- AMC 8/10/12/AIME Problems and Answers
- Why are Math Competitions Important to Girls?
- The Big Value of Middle School Math Competitions
- Great Benefits of Math Competitions
- A Little Competition Can Inspire Math Students to Greater Achievement
- Small-sized Class Instruction-focused Model
- Homework Correction is very Important — We Give an Extensive Correction of the Incorrect Answers of All Homework
- Homework assignments are a fundamental part of our courses
- Optimal Strategies to Solve Hard AMC Geometry Problems
- How to Solve Mathematics Problems
- Mathematics competitions are NOT mysterious, and every student can attend them! — 数学竞赛绝非神秘,每个学生都可参加!
- Girls should attend math competitions — 女生更应参加数学竞赛
- 2016 AMC 8 Results Announced — Eleven Students Received Perfect Scores
- 2015 AMC 8 Results Announced
- 2014 AMC 8 Winners for the U.S. Ivy League Education Center
- The Importance of Discrete Mathematics

Click HERE find out more about Math Competitions!
Click HERE to find out more about SAT Prep!






































 Homework
Homework


































 。
。